day 28 MLE and MAP
Likelihood(MLE와 MAP)
확률 변수로서의 모델 파라미터
아래는 파라미터 공간에서 두 점 aa, bb를 뽑아 y=ax+by=ax+b의 그래프를 그리는 코드입니다. 이론상으로는 실수 집합 전체에서 샘플링을 해야 하지만 코드로 구현하기가 불가능하고, 간단한 시각화를 위해 [-10, 10)[−10,10) 구간에서 샘플링했습니다.
import numpy as np
import matplotlib.pyplot as plt
parameter_points = []
fig1, axes1 = plt.subplots(2, 5, figsize=(10, 4))
for ax in axes1.flatten():
# np.random.uniform: 정해진 구간에서 수를 무작위로 추출하여 반환합니다.
a, b = np.random.uniform(-10, 10, size=2)
a = round(a, 3)
b = round(b, 3)
parameter_points.append((a, b))
x = np.linspace(-10, 10, 50)
y = a*x + b
ax.plot(x, y)
ax.set_title('y='+str(a)+'x'+'{0:+.03f}'.format(b))
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)
plt.tight_layout()
px, py = np.split(np.array(parameter_points), 2, axis=1)
fig2 = plt.figure()
axes2 = plt.gca()
axes2.set_title('samples from parameter space')
axes2.set_xlim(-10, 10)
axes2.set_ylim(-10, 10)
plt.scatter(px, py)
plt.show()
아래 코드는 평균이 (1,0)(1,0)이고 표준편차가 0.5인 정규분포에서 10개의 점을 무작위로 뽑은 다음, 대응되는 일차함수의 그래프를 각각 그려주는 코드입니다. 위쪽의 예제와 비교하면 파라미터 공간에서 추출된 샘플들이 (1,0)(1,0) 주위에 모여 있고, 결과 그래프들의 차이가 작은 것을 확인할 수 있습니다.
parameter_points = []
fig, axes1 = plt.subplots(2, 5, figsize=(10, 4))
for ax in axes1.flatten():
# np.random.normal: 정규분포를 따르는 확률 변수의 랜덤한 값을 반환합니다.
a, b = np.random.normal(loc=[1, 0], scale=0.5)
a = round(a, 3)
b = round(b, 3)
parameter_points.append((a, b))
x = np.linspace(-10, 10, 50)
y = a*x + b
ax.plot(x, y)
ax.set_title('y='+str(a)+'x'+'{0:+.03f}'.format(b))
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)
plt.tight_layout()
px, py = np.split(np.array(parameter_points), 2, axis=1)
fig2 = plt.figure()
axes2 = plt.gca()
axes2.set_title('samples from parameter space')
axes2.set_xlim(-10, 10)
axes2.set_ylim(-10, 10)
plt.scatter(px, py)
plt.show()

posterior와 prior, likelihood 사이의 관계
데이터를 관찰하기 전 파라미터 공간에 주어진 확률 분포 $p(θ)$를 prior(prior probability, 사전 확률)이라고 합니다.
만약 prior 분포를 고정시킨다면, 주어진 파라미터 분포에 대해서 우리가 갖고 있는 데이터가 얼마나 ‘그럴듯한지’ 계산할 수 값이 likelihood(가능도, 우도)입니다.
likelihood가 높다는 것은 곧 우리가 지정한 파라미터 조건에서 데이터가 관찰될 확률이 높다는 것이고, 데이터의 분포를 모델이 잘 표현하는 것이라고 생각할 수 있습니다.
likelihood 값을 최대화하는 방향으로 모델을 학습시키는 방법을 최대 가능도 추정(maximum likelihood estimation, MLE)이라고 합니다.
이 값을 ‘데이터를 관찰한 후 계산되는 확률’이라는 뜻에서 posterior(posterior probability, 사후 확률)라고 부릅니다.
이렇게 posterior를 최대화하는 방향으로 모델을 학습시키는 방법을 최대 사후 확률 추정(maximum a posteriori estimation, MAP)이라고 합니다. $(posterior= evidence likelihood×prior ,posterior∝likelihood×prior)$
## likelihood와 머신러닝

import math
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(321)
input_data = np.linspace(-2, 2, 5)
label = input_data + 1 + np.random.normal(0, 1, size=5)
plt.scatter(input_data, label)
plt.show()

# model: y = ax + b
# a, b 값을 바꾸면서 실행해보세요
#-------------------------------#
a = 1
b = 1
#-------------------------------#
# 모델 예측값
model_output = a*input_data + b
likelihood = []
# x: 입력데이터, y: 데이터라벨
# 예측값과 라벨의 차이를 제곱해 exp에 사용
for x, y, output in zip(input_data, label, model_output):
likelihood.append(1/(math.sqrt(2*math.pi*0.1*0.1))*math.exp(-pow(y-output,2)/(2*0.1*0.1)))
model_x = np.linspace(-2, 2, 50)
model_y = a*model_x + b
fig, ax = plt.subplots()
ax.scatter(input_data, label)
ax.plot(model_x, model_y)
for i, text in enumerate(likelihood):
ax.annotate('%.3e'%text, (input_data[i], label[i]))
plt.show()
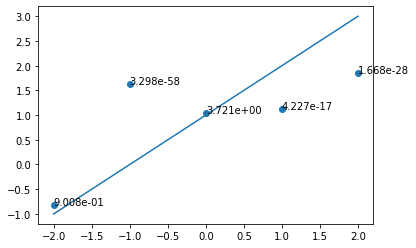
데이터 포인트가 모델 함수에서 멀어질수록 데이터의 likelihood는 기하급수적으로 감소합니다. likelihood를 구하는 식을 보면 모델 예측값과 데이터 라벨의 차이를 제곱해서 exponential 위에 올려놓은 것을 확인할 수 있습니다. 예측값과 라벨의 차이가 조금만 벌어져도 likelihood 값은 민감하게 반응하겠죠. 머신러닝의 목표가 데이터 포인트들을 최대한 잘 표현하는 모델을 찾는 것이었다는 사실을 생각하면, 결국 데이터 포인트들의 likelihood 값을 크게 하는 모델을 찾는 것이 됩니다. 데이터의 likelihood 값을 최대화하는 모델 파라미터를 찾는 방법이 최대 가능도 추론(maximum likelihood estimation, MLE)입니다
MLE 최대 가능도 추론
앞 스텝에서 데이터 포인트 하나의 likelihood 식을 살펴봤습니다. 모델 파라미터 $θ$가 주어졌을 때, 데이터 포인트의 likelihood는 다음과 같습니다.


MLE 최적해 구하기
아래 코드는 y=x+1y=x+1 함수를 기준으로 랜덤한 노이즈를 섞어서 데이터 포인트 20개를 생성하고 시각화하는 코드입니다. 데이터 생성 단계에서 지정한 노이즈의 분포는 평균이 0이고 표준편차가 0.5인 정규분포입니다.
import math
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
num_samples = 20
input_data = np.linspace(-2, 2, num_samples)
labels = input_data + 1 + np.random.normal(0, 0.5, size=num_samples)
plt.scatter(input_data, labels)
plt.show()
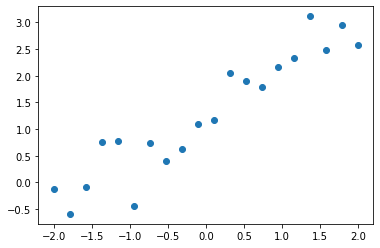
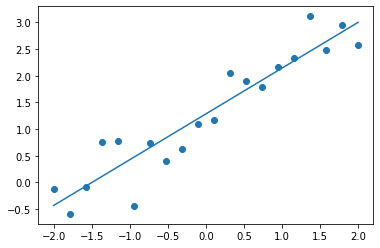
아래 코드로 구한 최적의 모델은 y=0.8578x+1.2847y=0.8578x+1.2847입니다. 데이터 포인트들이 y=x+1y=x+1 함수로부터 생성된 것을 생각하면 꽤 가까운 결과가 나왔습니다.
def likelihood(labels, preds):
result = 1/(np.sqrt(2*math.pi*0.1*0.1))*np.exp(-np.power(labels-preds,2)/(2*0.1*0.1))
return np.prod(result)
def neg_log_likelihood(labels, preds):
const_term = len(labels)*math.log(1/math.sqrt(2*math.pi*0.1*0.1))
return (-1)*(const_term + 1/(2*0.1*0.1)*np.sum(-np.power(labels-preds,2)))
# X: 20x2 matrix, y: 20x1 matrix
# input_data 리스트를 column vector로 바꾼 다음 np.append 함수로 상수항을 추가합니다.
X = np.append(input_data.reshape((-1, 1)), np.ones((num_samples, 1)), axis=1)
y = labels
theta_1, theta_0 = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), y)
print('slope: '+'%.4f'%theta_1+' bias: '+'%.4f'%theta_0)
predictions = theta_1 * input_data + theta_0
print('likelihood: '+'%.4e'%likelihood(labels, predictions))
print('negative log likelihood: '+'%.4e'%neg_log_likelihood(labels, predictions))
model_x = np.linspace(-2, 2, 50)
model_y = theta_1 * model_x + theta_0
plt.scatter(input_data, labels)
plt.plot(model_x, model_y)
plt.show()
slope: 0.8578 bias: 1.2847
likelihood: 2.9724e-54
negative log likelihood: 1.2325e+02
MLE와 MAP의 비교
MAP는 MLE와 비슷하지만 정규화 항에 해당하는 negative log prior 부분이 존재한다는 차이가 있었습니다. 그래서 MLE 모델보다 MAP 모델이 더 안정적이라는 이야기를 했었죠.
이상치 데이터 한 개를 데이터 포인트 20개에 추가하는 것으로는 모델에 큰 영향을 주지 못해서 데이터 포인트를 10개로 줄이고 이상치 데이터도 2개 추가합니다.
import math
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
num_samples = 10
input_data = np.linspace(-2, 2, num_samples)
labels = input_data + 1 + np.random.normal(0, 0.5, size=num_samples)
input_data = np.append(input_data, [0.5, 1.5])
labels = np.append(labels, [9.0, 10.0])
plt.scatter(input_data, labels)
plt.show()
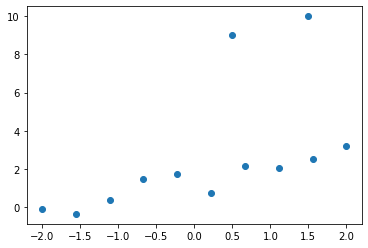

def likelihood(labels, preds):
result = 1/(np.sqrt(2*math.pi*0.1*0.1))*np.exp(-np.power(labels-preds,2)/(2*0.1*0.1))
return np.prod(result)
def neg_log_likelihood(labels, preds):
const_term = len(labels)*math.log(1/math.sqrt(2*math.pi*0.1*0.1))
return (-1)*(const_term + 1/(2*0.1*0.1)*np.sum(-np.power(labels-preds,2)))
# X: 21x2 matrix, y: 21x1 matrix
# input_data 리스트를 column vector로 바꾼 다음 np.append 함수로 상수항을 추가합니다.
X = np.append(input_data.reshape((-1, 1)), np.ones((num_samples+2, 1)), axis=1)
y = labels
# MLE 파라미터 계산식
mle_theta_1, mle_theta_0 = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), y)
# MAP 파라미터 계산식
map_theta_1, map_theta_0 = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)+(0.1*0.1)/(0.04*0.04)*np.eye(2)), X.T), y)
print('[MLE result] (blue)')
print('slope: '+'%.4f'%mle_theta_1+' bias: '+'%.4f'%mle_theta_0)
mle_preds = mle_theta_1 * input_data + mle_theta_0
print('likelihood: '+'%.4e'%likelihood(labels, mle_preds))
print('negative log likelihood: '+'%.4e\n'%neg_log_likelihood(labels, mle_preds))
print('[MAP result] (orange)')
print('slope: '+'%.4f'%map_theta_1+' bias: '+'%.4f'%map_theta_0)
map_preds = map_theta_1 * input_data + map_theta_0
print('likelihood: '+'%.4e'%likelihood(labels, map_preds))
print('negative log likelihood: '+'%.4e'%neg_log_likelihood(labels, map_preds))
model_x = np.linspace(-2, 2, 50)
mle_model_y = mle_theta_1 * model_x + mle_theta_0
map_model_y = map_theta_1 * model_x + map_theta_0
plt.scatter(input_data, labels)
plt.plot(model_x, mle_model_y)
plt.plot(model_x, map_model_y)
plt.show()
[MLE result] (blue)
slope: 1.4748 bias: 2.4784
likelihood: 0.0000e+00
negative log likelihood: 4.1298e+03
[MAP result] (orange)
slope: 1.1719 bias: 1.6628
likelihood: 0.0000e+00
negative log likelihood: 4.6645e+03
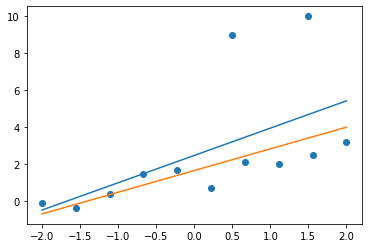
위 그래프에서 파란색 직선과 주황색 직선은 각각 MLE, MAP를 이용해 찾은 모델을 나타냅니다. 파란색 직선은 이상치 데이터까지 포함한 negative log likelihood를 감소시키기 위해 직선이 위로 치우쳐서 아래쪽 10개 데이터의 경향성에서는 약간 벗어났습니다. 반면 주황색 직선은 이상치 데이터가 추가되어도 아래쪽 데이터에서 크게 벗어나지는 않고 있습니다.
원래 데이터 분포에서 멀리 떨어진 이상치 데이터가 추가되었기 때문에, likelihood의 값은 언더플로우가 발생해서 0으로 표시됩니다. negative log likelihood의 값을 보면 MLE 결과와 MAP 결과를 비교할 수 있습니다. MAP가 MLE에 비해 negative log likelihood 값이 크지만(likelihood가 작지만), 이상치 데이터가 추가되었을 때 모델 파라미터의 변화는 MLE보다 작습니다.
Leave a comment